قانون مساحة المثلث متساوي الساقين

المثلث متساوي الساقين

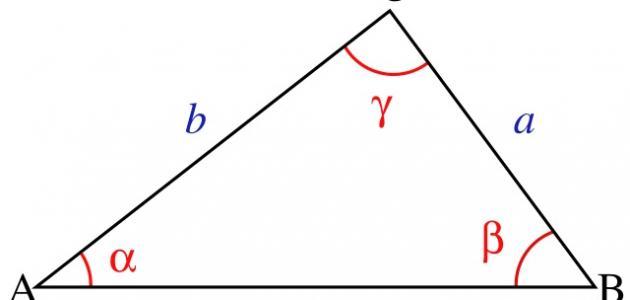
إنّ المثلث متساوي الساقين هو شكل هندسي ثنائي الأبعاد مكوّن من ثلاثة رؤوس تصل بينها ثلاثة أضلاع، وهو حالة خاصة للمثلث حيث إنّ له ضلعين متساويين وتكون الزاويتان المقابلتان لهذين الضلعين متساويتين أيضاً، ولهذا المثلث خصائص تميزه عن غيره من الأشكال الهندسيّة، كما أنّ له قانوناً خاصاً لحساب مساحته، وهو ما سنتحدث عنه في مقالنا هذا.

خصائص المثلث متساوي الساقين

• يحتوي على ضلعين متساويين في الطول.
• يكون ضلع المثلث الثالث مُختلفاً في طوله عن الضلعين الآخرين، وهو يُمثّل قاعدة المثلث متساوي الساقين.
• تُسمى الزاوية المقابلة للضلع الثالث برأس المثلث.
• تكون زاويتا القاعدة حادتين ومتساويتين في القياس.
• يشكّل الخط المستقيم الواصل من رأس المثلث إلى منتصف القاعدة ارتفاع المثلث.
• يُسمى العمود النازل من رأس الزاوية والذي ينصفها وينصف قاعدة المثلث بالعمود بالمتوسط.

قانون مساحة المثلث متساوي الساقين

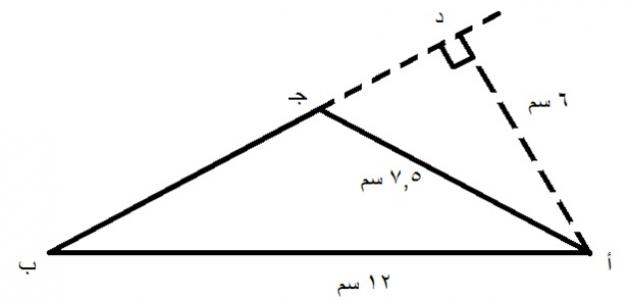
إنّ مساحة المثلث متساوي الساقين هو: مساحة المثلث=1/2×طول قاعدة المثلث×ارتفاع المثلث، حيث إنّ قاعدة المثلث في حالة المثلث متساوي الساقين التي تُمثّل طول الضلع المختلِف في طوله عن الضلعين الآخرين المتساويين، كما أنّ ارتفاع المثلث المتساوي الساقين هو طول العمود النازل على هذه القاعدة أو على امتدادها من الرأس المقابل لها.

أمثلة لحساب مساحة المثلث متساوي الساقين مثال (1) مثلث متساوي الساقين طول كلّ ضلع من ضلعيه المتساويين يساوي 5سم، وطول ضلعه الثالث يساوي 6سم، وطول العمود النازل من رأس هذا المثلث على ضلعه الثالث يساوي 4سم، أوجد مساحته؟

الحل:

• مساحة المثلث=1/2×طول قاعدة المثلث×ارتفاع المثلث.
• طول ضلع المثلث الثالث يُمثّل طول القاعدة ويساوي 6سم.
• طول العمود النازل من رأس المثلث على قاعدته يُمثّل ارتفاع المثلث ويساوي 4سم.
• مساحة المثلث=1/2×6×4=12سم2.

مثال (2) إذا علمت أنّ طول قاعدة مثلث متساوي الساقين تساوي 10سم، ومساحته تساوي 60سم2، فما ارتفاع المثلث؟

الحل:

• مساحة المثلث=1/2×طول قاعدة المثلث×ارتفاع المثلث.
• 60=1/2×10×ارتفاع المثلث.
• 60=5×ارتفاع المثلث.
• ارتفاع المثلث=60/ 5=12سم.

مثال (3) مثلث متساوي الساقين طول قاعدته تساوي 12سم، وطول كلّ ضلع من ضلعيه المتساويين يساوي 10سم، أوجد مساحة المثلث؟

الحل:

مساحة المثلث=1/2×طول قاعدة المثلث×ارتفاع المثلث.

مساحة المثلث=1/2×12×ارتفاع المثلث.

لإيجاد ارتفاع المثلث متساوي الساقين نُطبّق نظرية فيثاغوروس على المثلث قائم الزاوية المتكوّن من إنزال عمود من الرأس إلى منتصف القاعدة، وتنص النظرية على:

• طول الوتر2=طول الضلع الأول2+طول الضلع الثاني2.
• طول الوتر يُمثّل طول أحد الضلعين المتساويين، وطول الضلع الأول هو طول نصف القاعدة، أما طول الضلع الثاني فيُمثّل ارتفاع المثلث.
• 102 62+طول الضلع الثاني2.
• 100=36+طول الضلع الثاني2.
• طول الضلع الثاني2 64.
• طول الضلع الثاني=ارتفاع المثلث=الجذر التربيعي ل64=8سم.
• مساحة المثلث=1/2×12×ارتفاع المثلث.
• مساحة المثلث=1/2×12×8.
• مساحة المثلث=48سم2.